Manifold Learning
Nonlinear dimensionality reduction.
Inputs
- Data: input dataset
Outputs
- Transformed Data: dataset with reduced coordinates
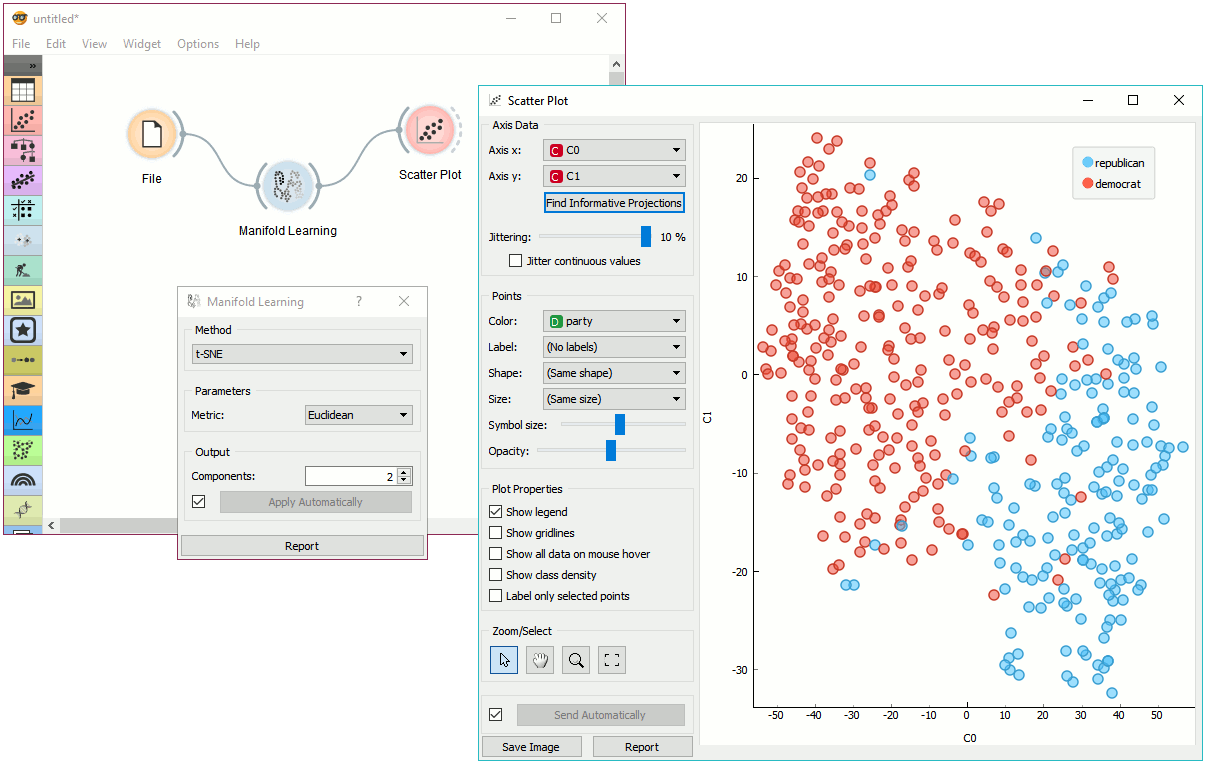
Manifold Learning is a technique which finds a non-linear manifold within the higher-dimensional space. The widget then outputs new coordinates which correspond to a two-dimensional space. Such data can be later visualized with Scatter Plot or other visualization widgets.
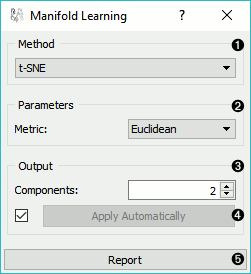
- Method for manifold learning:
- Set parameters for the method:
- t-SNE (distance measures):
- Euclidean distance
- Manhattan
- Chebyshev
- Jaccard
- Mahalanobis
- Cosine
- MDS (iterations and initialization):
- max iterations: maximum number of optimization interactions
- initialization: method for initialization of the algorithm (PCA or random)
- Isomap:
- number of neighbors
- Locally Linear Embedding:
- method:
- standard
- modified
- hessian eigenmap
- local
- number of neighbors
- max iterations
- method:
- Spectral Embedding:
- affinity:
- nearest neighbors
- RFB kernel
- affinity:
- t-SNE (distance measures):
- Output: the number of reduced features (components).
- If Apply automatically is ticked, changes will be propagated automatically. Alternatively, click Apply.
- Produce a report.
Manifold Learning widget produces different embeddings for high-dimensional data.
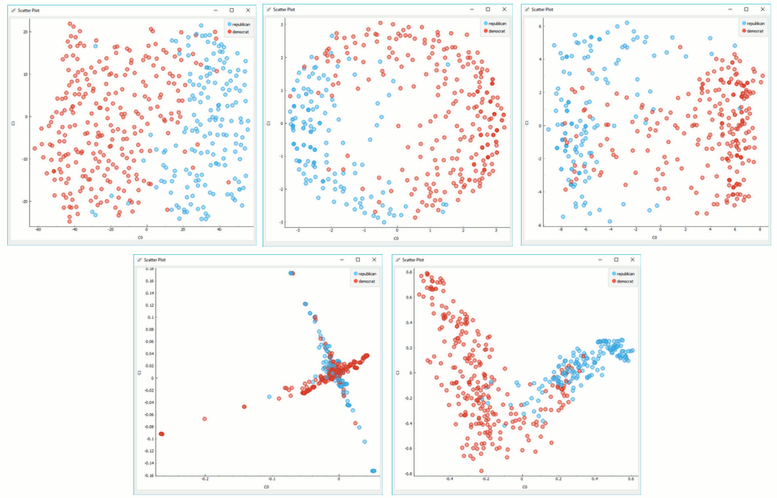
From left to right, top to bottom: t-SNE, MDS, Isomap, Locally Linear Embedding and Spectral Embedding.
Preprocessing
All projections use default preprocessing if necessary. It is executed in the following order:
- continuization of categorical variables (with one feature per value)
- imputation of missing values with mean values
To override default preprocessing, preprocess the data beforehand with Preprocess widget.
Example
Manifold Learning widget transforms high-dimensional data into a lower dimensional approximation. This makes it great for visualizing datasets with many features. We used voting.tab to map 16-dimensional data onto a 2D graph. Then we used Scatter Plot to plot the embeddings.